Questa è tosta. Mettetevela via subito, che qui c’è da sgobbare sul serio perché questa è tosta forte, ma ne varrà la pena. Partiamo dal principio con una confessione: tutto questo lavoraccio con GDExtension è nato per una mia esigenza personale. E’ da tempo che cerco soluzioni per generare pianeti procedurali. Si tratta di un qualcosa che desidero fare da un po’, senza un motivo particolare. La verità è che ci sono riuscito, non meno di cinque dannate volte! Ho le prove: vedete Vid.1. Quello nel video è, sicuramente, il tentativo migliore riuscito. Si tratta di un pianeta costruito al volo mentre lo si esplora.
Da un punto di vista grafico, è una semisfera con il polo sempre puntato verso la telecamera, che si ridisegna in base alla posizione dell’osservatore. Anche se nel video sembra il contrario, ha un grosso problema: è lento. Ho usato i thread e persino due mesh che si scambiano di posto, sicché mentre l’una è visualizzata, l’altra è in costruzione. Però, c’è sempre il problema della lentezza: se si va troppo veloci, la mesh non ce la fa a ridisegnarsi in tempo e si raggiungono i confini. Allora ho pensato: “Faccio tutto con gli shader, no?”… Niente da fare. Gli shader si portano dietro il problema di una pessima gestione delle normali, visto che si ha accesso al singolo punto per volta, ma non ai triangoli che permettono di calcolare delle normali decenti.
Così ho pensato a GDExtension, come ultima spiaggia. Ne è scaturito tutto questo popò di lavoro, che non è nient’altro se non un grosso blocco degli appunti dedicato a quello che c’è da sapere per GDExtension in generale, ma che ha il fine ultimo di mettermi in grado di ricreare quello stesso lavoro, questa volta davvero funzionante…
Organizzare i dati
La parte più complicata di questo benchmark è capire come si costruisce un terreno a partire dal nulla. Potevo buttarvi li il codice e basta, ma mi sembrava poco carino, soprattutto considerando che questo è un tutorial. Date le premesse e tenendo presente la filosofia dell’uso di GDExtension solo ed esclusivamente in casi di emergenza, un senso a tutto questo lavoro dovevo darlo, no? Eccolo! Sarà lunghetta, preparatevi. Vi spiego come funziona il codice in GDScript, tanto in C++ è praticamente identico: potete guardarvelo da soli, che vale pure come allenamento.
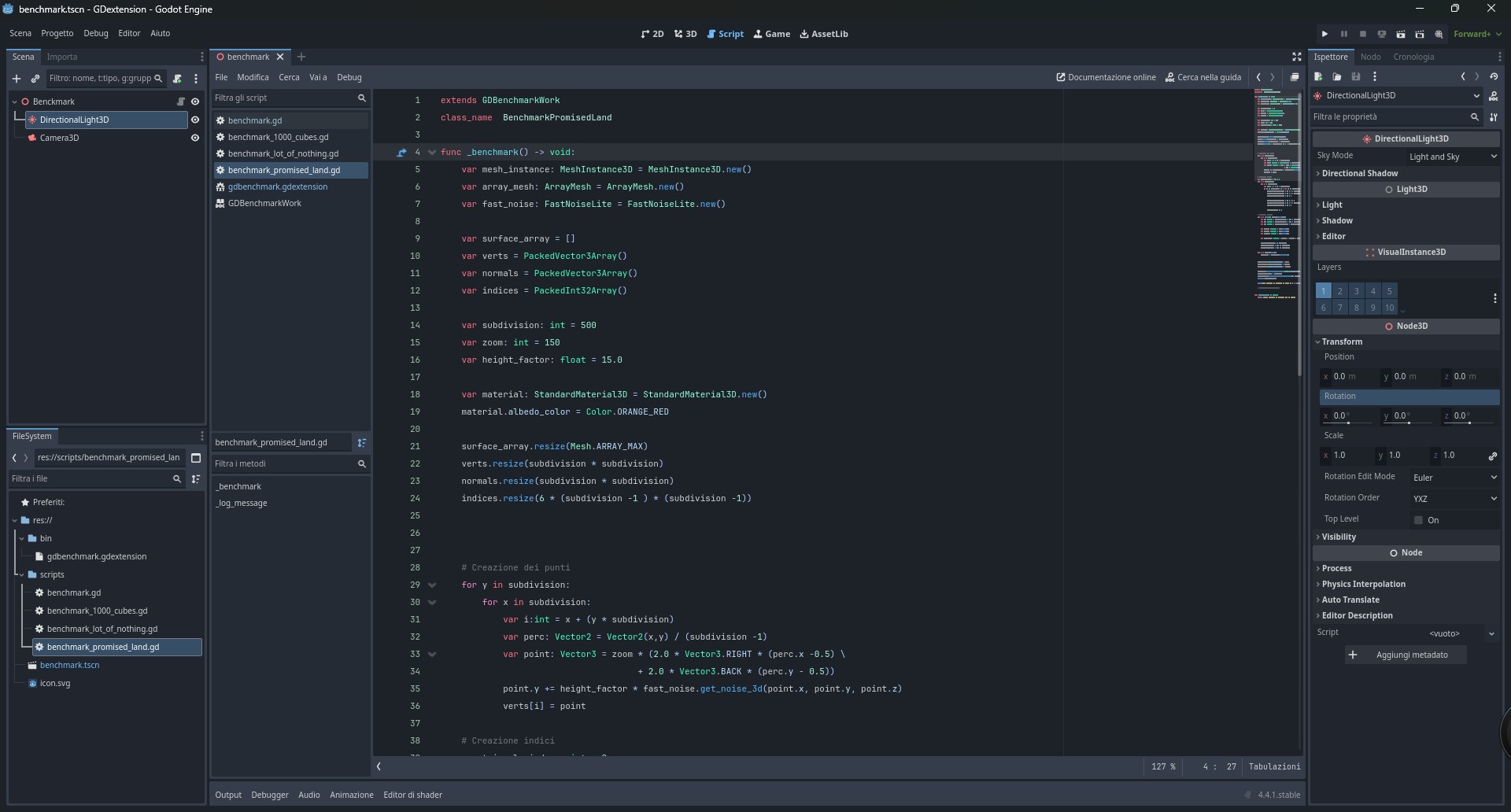
Uno dei metodi per generare una mesh totalmente procedurale tra i più gettonati, è quello che sfrutta un ArrayMesh. Per capire come creare la geometria finale, ArrayMesh chiede in pasto un array di array, dove ognuna delle posizioni è dedicata ad una tipologia particolare di dati. Per puntare il giusto array, ci sono una serie di costanti come Mesh.ARRAY_VERTEX che potete divertirvi a stampare, così tanto per capirne il funzionamento interno. La prima cosa che ci occorre per prepararci a costruire un terreno tutto nostro, è un array che contenga i dati necessari. Nel codice, sotto il metodo _benchmark come al solito, a partire dalla riga 9, trovate queste istruzioni:
var surface_array = []
var verts = PackedVector3Array()
var normals = PackedVector3Array()
var indices = PackedInt32Array()surface_array sarà il nostro contenitore di tutti i dati necessari. Gli altri tre array ci serviranno, ognuno, per uno scopo ben preciso. Noterete che, a parte surface_array, sono tutti packed array, cioè array studiati per ottimizzare l’uso della memoria, ma che sono meno user friendly di quelli che usiamo solitamente, per contro. I tipi di packed array utilizzati, non sono casuali: una tabella nella guida ufficiale1, chiarisce quale tipo di dato ArrayMesh si aspetta per quale scopo. Nel nostro caso abbiamo dato nome verts all’array che useremo per memorizzare i vertici della figura, normals a quello delle normali e indices a quello per gli indici dei triangoli (tranquilli che capite dopo…).
Facciamo un salto in avanti, alla riga 21. Troviamo questo codice:
surface_array.resize(Mesh.ARRAY_MAX)
verts.resize(subdivision * subdivision)
normals.resize(subdivision * subdivision)
indices.resize(6 * (subdivision -1 ) * (subdivision -1))subdivision è un intero con valore arbitrario che rappresenta il numero di righe e colonne (se così si può dire) della nostra superficie che sarà, ovviamente, quadrata. Non è che sia obbligatorio, ma in genere, parlando di terreni, ne rende più semplice la creazione. Come vedete, surface_array viene ridimensionato ad un valore ben preciso: Mesh.ARRAY_MAX. Si tratta di una costante che magari in futuro potrebbe cambiare, ma al momento vale 13, perché tali sono le tipologie di array che si possono creare per personalizzare la propria mesh.
verts conterrà i punti che costituiscono la mesh finale e, non a caso, è un PackedVector3Array, perché dovrà contenere coordinate tridimensionali. Credo sia abbastanza chiaro perché è stato ridimensionato al quadrato del numero di suddivisioni, vero?
normals potrebbe essere un po’ meno chiaro, ma ha le stesse dimensioni di verts semplicemente perché, ad ogni punto, farà corrispondere la sua normale.
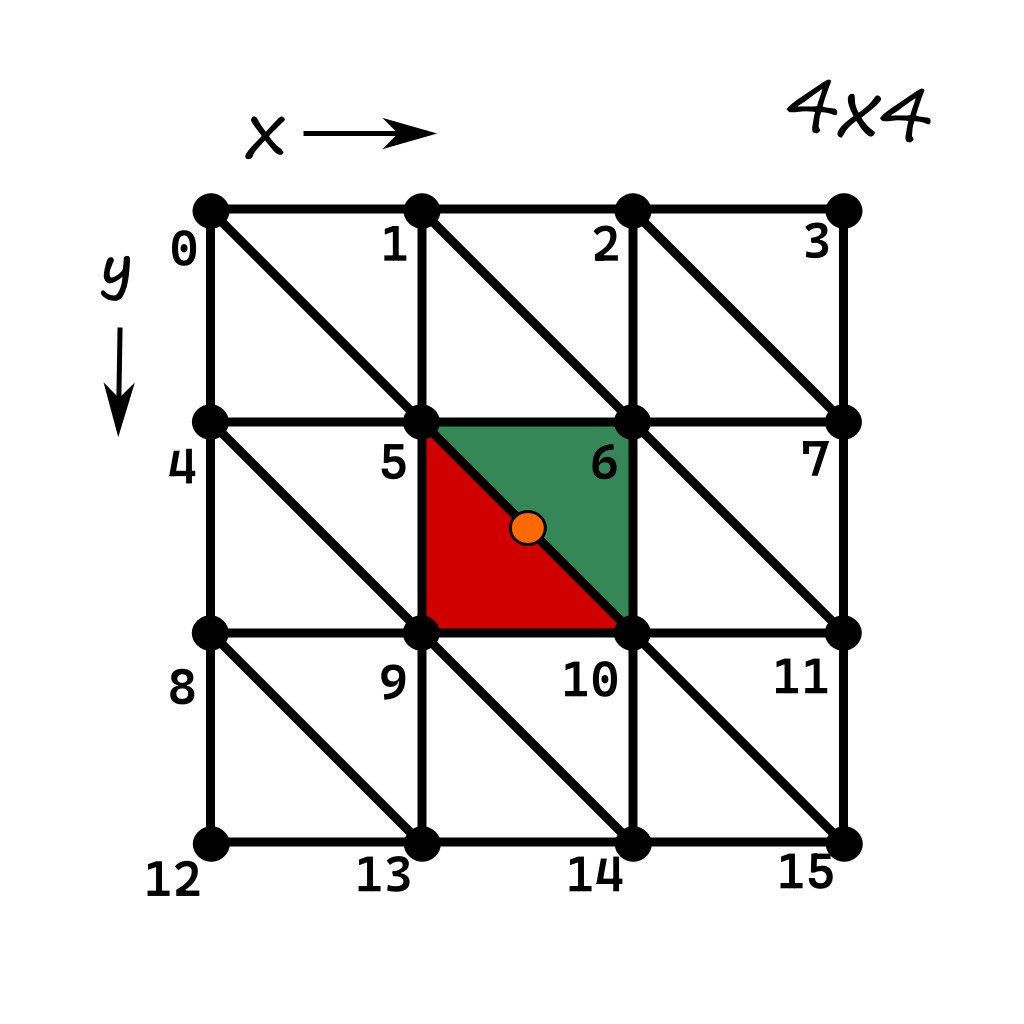
indices, invece, non potete capirlo da soli. Dovete sapere che il mondo è fatto di triangoli. indices è un array che serve a mettere insieme i punti in verts per farli diventare triangoli, appunto. Guardate Fig.20: ho preparato uno schema a cui ci riferiremo spesso. Se ci fate caso, ogni riga e ogni colonna è formato da un certo numero di quadrati. I quadrati sono tanti quanto gli spazi tra i punti, quindi subdivision-1.
Ogni quadrato è formato da due triangoli. Lasciate perdete il vostro intuito: matematicamente, ogni triangolo ha 3 vertici che diventano 6 se i triangoli sono due: il computer non capisce il concetto di congruenza. Ecco spiegato da dove viene la dimensione di indices.
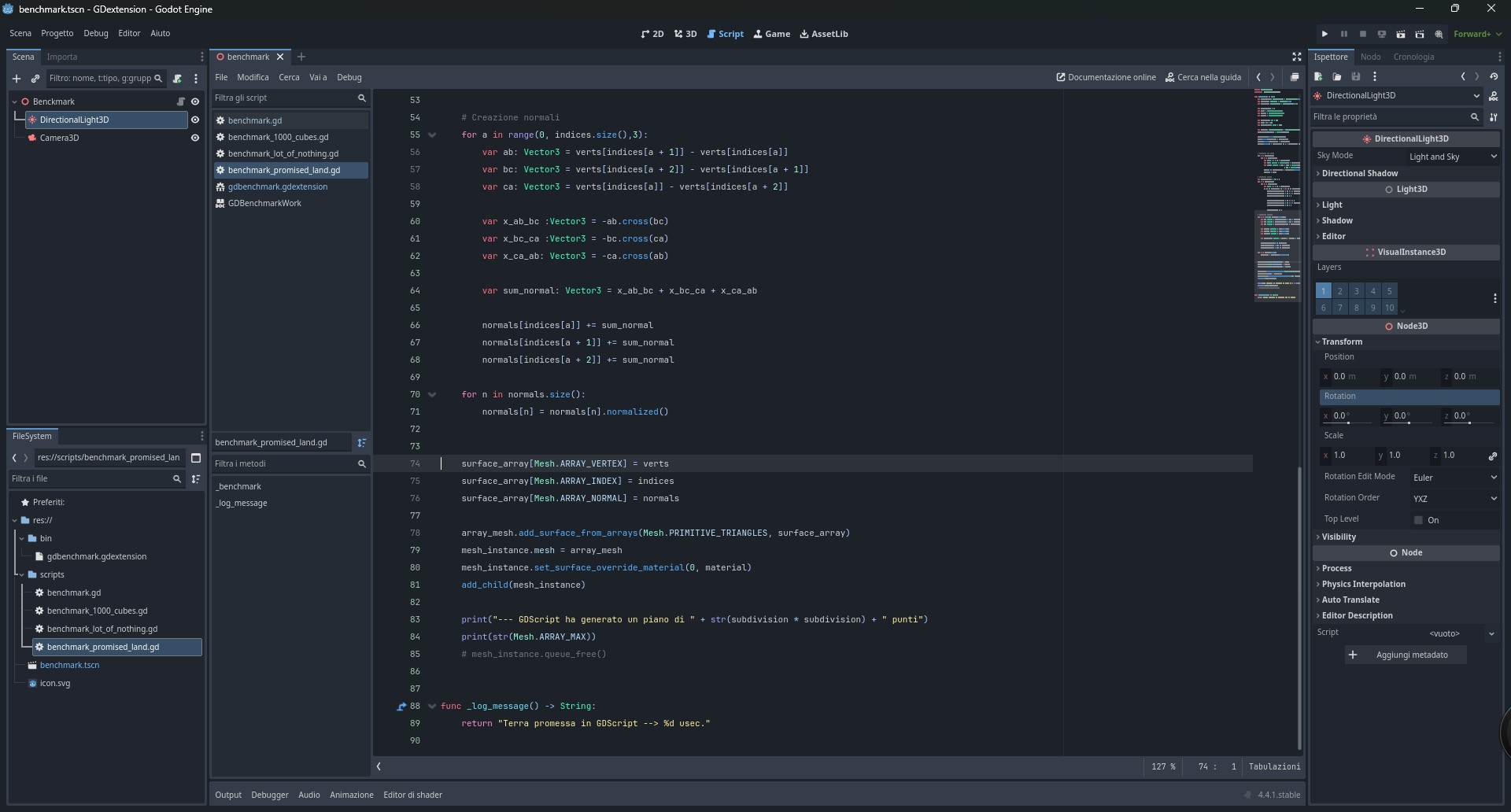
Adesso saltiamo di sana pianta tutto, ed arriviamo, direttamente, alla riga 74 del codice (Fig.19), dove troviamo queste istruzioni:
surface_array[Mesh.ARRAY_VERTEX] = verts
surface_array[Mesh.ARRAY_INDEX] = indices
surface_array[Mesh.ARRAY_NORMAL] = normals
array_mesh.add_surface_from_arrays(Mesh.PRIMITIVE_TRIANGLES, surface_array)Come vedete, in corrispondenza di indici definiti con costanti, surface_array riceve tutti quelli gestiti in precedenza. Potete immaginare surface_array come uno scaffale con i ripiani sovrapposti, ognuno dei quali con la sua targhetta. In ogni ripiano viene infilato l’array che corrisponde a quella targa.
Alla fine, non resta che passare i dati alla mesh di tipo ArrayMesh: si fa con un metodo all’uopo, add_surface_from_arrays che accetta, come parametri, una costante che stabilisce come debbano essere trattate le informazioni e il nostro array di array. In teoria, è possibile disegnare una mesh fatta da punti sparsi o con sole linee, tipo wireframe. Noi usiamo il metodo classico che si avvale di triangoli.
Facciamo i calcoli
Le singole coordinate
Dovremmo aver capito come funzionano gli array usati per creare la mesh, grosso modo, ma non li abbiamo ancora riempiti. Quello che faremo, questa volta, è riempire i tre packed array creati in precedenza. Queste operazioni passano per dei cicli bidimensionali, per cui risultano essere parecchio onerose in termini di tempo di elaborazione. Ecco perché, parlando di mesh costruite al volo, GDExtension può dare un grosso aiuto: abbiamo un lavoro misto tra chiamate al game engine e calcoli veri e propri.
Vediamo come procedere, adesso. Partiamo dal ciclo che si incontra alla linea 29 (Fig.22).
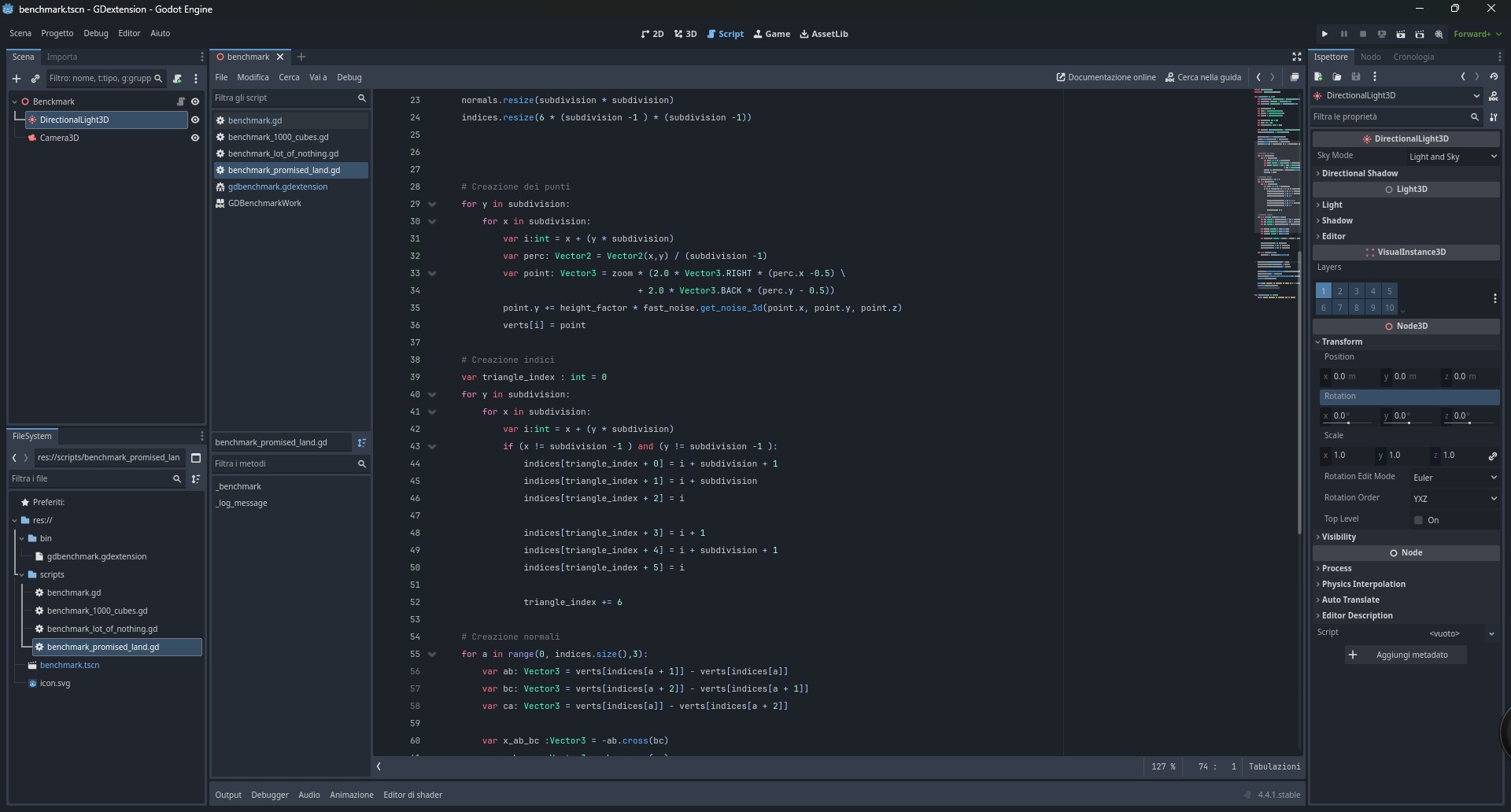
for y in subdivision:
for x in subdivision:
var i:int = x + (y * subdivision)
var perc: Vector2 = Vector2(x,y) / (subdivision -1)
var point: Vector3 = zoom * (2.0 * Vector3.RIGHT * (perc.x -0.5) \
+ 2.0 * Vector3.BACK * (perc.y - 0.5))
point.y += height_factor * fast_noise.get_noise_3d(point.x, point.y, point.z)
verts[i] = point Se vi aiutate con la Fig.20, noterete che x rappresenta un asse, y l’altro. La variabile i, assume un valore calcolato da x e y. Se provate a mano, scoprirete che scorre tutta la griglia dei punti, indicandoli con un numero che corrisponde a quelli in figura. Dato il funzionamento del ciclo for, y non assumerà mai il valore di subdivision, ma al massimo subdivision -1. In pratica, abbiamo ridotto una griglia ad una array lineare, quale è un PackedVector3Array().
perc è un Vector2. Se vedete il calcolo per crearlo, doveste rendervi conto che contiene la posizione di un punto in termini percentuali. In altre parole, sia perc.x che perc.y potranno assumere solo valori che vanno da 0 ad 1.
Apriamo una parentesi. Di solito è bene creare le mesh con le singole coordinate entro valori compresi tra -1 e 1. E’ sufficiente moltiplicare ogni coordinata per un valore qualsiasi per ottenere un effetto zoom che fa assumere alla mesh le dimensioni desiderate. Se date un’occhiata a Fig.18, scoprirete che abbiamo creato un parametro chiamato proprio zoom con valore 150. Significa che la nostra griglia finale, avrà dimensioni di 300×300 punti, con range tra -150 e 150 in termini di coordinate.
Vediamo com’è stato creato point, il punto di nostro interesse. La “\” serve solo per concatenare righe secondo gli standard sintattici di GDScript e, quindi, fate finta che non ci sia. Abbiamo due addendi. Uno è questo:
2.0 * Vector3.RIGHT * (perc.x -0.5)Vogliamo una mesh con coordinate tra -1 e 1, giusto? Vogliamo anche che sia centrata nel punto (0,0,0) dello spazio. Partiamo dal presupposto che perc.x e perc.y possono assumere valori tra 0 e 1. Se gli sottraiamo -0.5, i valori cambiano range e si collocano tra -0.5 e 0.5. Moltiplicate per 2 ed il gioco è fatto. Vector3.Right? E’ un vettore con coordinate (1,0,0). Per effetto del resto del calcolo, perc.x avrà valori che si muovono da -1 a 1, giusto? Allora questa riga restituirà valori compresi tra (-1,0,0) e (1,0,0). L’altra riga si comporta allo stesso modo, ma crea i valori sull’asse z. Vector3.Back, infatti, vale (0,0,1). Andando a sommare tra di loro le due righe, abbiamo coordinate comprese tra (-1,0,-1) e (1,0,1). Notate che y rimane sempre a zero: la superficie è piatta, per il momento. Ricordate che c’è zoom che moltiplica la somma dei vettori, e cambia le dimensioni di tutta la mesh. Guardate ora:
point.y += height_factor * fast_noise.get_noise_3d(point.x, point.y, point.z)Tornate a dare un’occhiata a Fig.18, molto in alto in questa pagina. Noterete che fast_noise è stato creato subito in testa al metodo ed è un oggetto di classe FastNoiseLite. Si tratta di un generatore di texture pseudo-casuali. Lo abbiamo tenuto così com’è, con i suoi valori di default. Semplicemente, andiamo a prenderci il valore di noise passando le coordinate del punto, appena calcolate. Le moltiplichiamo per height_factor, un valore creato anch’esso nella parte alta del codice, del tutto arbitrario, che serve ad aumentare l’effetto della noise map, eventualmente a ridurlo. Cosa otterremo? Montagne! Il valore lo applichiamo solo all’asse y, che precedentemente era costretto a 0.
Alla fine, come vedete, il singolo punto così calcolato, viene inserito nel vettore verts[i].
Questi dannati indici
Veniamo agli indici, quella cosa che avevo detto essere un po’ strana. Nel precedente spezzone di codice, abbiamo riempito l’array verts con i singoli punti che compongono il nostro terreno. Adesso, in qualche modo, dobbiamo far capire a Godot dove sono i triangoli, perché da solo non ci arriva. Prendiamo questo codice, che trovate nella parte mediana di Fig.22:
var triangle_index : int = 0
for y in subdivision:
for x in subdivision:
var i:int = x + (y * subdivision)
if (x != subdivision -1 ) and (y != subdivision -1 ):
indices[triangle_index + 0] = i + subdivision + 1
indices[triangle_index + 1] = i + subdivision
indices[triangle_index + 2] = i
indices[triangle_index + 3] = i + 1
indices[triangle_index + 4] = i + subdivision + 1
indices[triangle_index + 5] = i
triangle_index += 6Si tratta proprio del ciclo che costruisce gli indici. La prima cosa che si nota è questo triangle_index, un indice, chiaramente, ma… non ci bastavano x e y? All’ultima riga, vedete questo strano incremento di 6 unità: vuoi vedere che sono i due triangoli per quadrato di prima? Lasciamolo lievitare e prendiamola larga. Vi conviene simulare a mente quello che vi dirò, aiutandovi con la Fig.22, che poi è lo stesso schema di Fig.20 riportato per comodità.
Come si dice a Godot dove sono i triangoli? Se l’array si chiama indices, non è un caso. Contiene indici riferiti a verts, l’array delle coordinate pure. indices va letto come se fosse una sequenza di informazioni a gruppi di tre. Adesso, farlo a mano è roba da far venire il mal di testa, ovviamente, ma parlando sul piano teorico, il primo triangolo è nascosto nelle prime tre posizioni. Supponiamo di creare proprio il piano di Fig.22, dove subdivision vale 4: noi ovviamente desideriamo un piano fatto da centinaia di punti, ma prendiamocela con questo miserabile piano 4×4 giusto per capire l’algoritmo alla base di tutto. Se andaste a stamparvi i primi tre valori di indices, trovereste questa sequenza di interi: [5, 4, 0]. Come si leggono? Si tratta degli indici, appunto, da dare a verts per costruire il primo triangolo. Il primo triangolo, quindi ha coordinate:
verts[5], verts[4], verts[0]Cosa un po’ strana nella vita reale, ma per niente in computer grafica, è che le facce dei solidi si possono vedere solo da un lato. Supponiamo di osservare e vedere questo triangolo dall’alto, spostando la telecamera per vederlo dal basso ci risulterebbe del tutto trasparente: è un espediente per risparmiare in tempi di rendering, come ce ne sono altri. Ci servirebbe un altro numero, a questo punto, per indicare il verso del triangolo, no? Invece viene usata una convenzione: si usa rappresentare le sequenze di indici in senso orario per mostrare le facce orientate verso le loro normali ed in senso antiorario per ottenere l’effetto opposto. Quindi la sequenza [5, 4, 0] funzionerebbe anche se fosse [0, 5, 4] (seguite la Fig.22), ma non se fosse [4, 5, 0]. Chiaro, no? No, ovviamente: perché non abbiamo ancora costruito le normali, ma abbiate fiducia, punteranno nel verso giusto.

Ora, se vi andate a rivedere il codice, scoprirete che, in questo ciclo come nel precedente, a partire da x e y viene costruito un indice i che scorre tutti i punti che costituiscono il piano. In corrispondenza di ogni valore di i vengono creati gli indici di cui i è lo spigolo in alto a sinistra stando alla Fig.22. Per ogni valore di i, quindi, verrà creata la seguente sequenza di indici:
[ i+subdivision+1, i+subdivision, i, i+1, i+subdivision+1, i]Ho colorato due triangoli, in Fig.22. Fanno riferimento, secondo quando detto sino ad ora, all’indice di valore 5. Tenendo presente che, nella figura, subdivision vale 4, se assegnamo ad i il valore 5, allora gli indici del quadrato costituito dalla somma dei due triangoli è:
[10, 9, 5, 6, 10, 5]Provare per credere. Soprattutto, provare con qualsiasi valore di i per vedere che funziona sempre… Quasi sempre. Vale se x e y non hanno valore pari a subdivision-1, da cui l’if che compare nel codice. Per capirlo, vi conviene provare a manina la sequenza, eseguire il codice a mente! Solo così finirete per capirlo bene.
Adesso è comprensibile perché c’è un triangle_index che viene incrementato di 6 unità ad ogni ciclo: semplicemente perché, ad ogni punto ovvero per ogni valore di i, faremo corrispondere qualcosa come 6 indici per ricostruire, ogni volta, due triangoli.
Le normali
E’ il momento di costruire le normali. Adesso capirete perché, in uno shader, non si riesce ad ottenere lo stesso effetto che si ottiene con ArrayMesh nella ricostruzione delle normali: gli shader vi mettono a disposizione un punto per volta, ma a noi ne servono tre, quelli che in ogni triangolo compongono la figura intera. Prendiamoci il codice corrispondente:
for a in range(0, indices.size(), 3):
var ab: Vector3 = verts[indices[a + 1]] - verts[indices[a]]
var bc: Vector3 = verts[indices[a + 2]] - verts[indices[a + 1]]
var ca: Vector3 = verts[indices[a]] - verts[indices[a + 2]]
var x_ab_bc :Vector3 = -ab.cross(bc)
var x_bc_ca :Vector3 = -bc.cross(ca)
var x_ca_ab: Vector3 = -ca.cross(ab)
var sum_normal: Vector3 = x_ab_bc + x_bc_ca + x_ca_ab
normals[indices[a]] += sum_normal
normals[indices[a + 1]] += sum_normal
normals[indices[a + 2]] += sum_normal
for n in normals.size():
normals[n] = normals[n].normalized()
Il primo ciclo, assegna valori ad a che, partendo da zero, vanno fino alla lunghezza dell’array di indici a gruppi di tre. Non vi spiego neanche il motivo: se non ci arrivate, ricominciate da capo.
Se vi ricordate, avevamo detto che l’array indices cominciava con la sequenza [5, 4, 0]. Guardate la Fig. 23, sempre la solita dello schema, riportata ancora una volta perché ce l’abbiate sempre sotto il naso.
Se leggete bene il codice, scoprirete che ab non è nient’altro che un vettore rappresentante la direzione che, partendo dal punto con indice 5, arriva a quello con indice 4. bc parte dal punto con indice 0 e arriva, anche lui, al punto con indice 4.
Passiamo alla definizione di x_ab_bc, scopriamo che si tratta del cross product tra i due vettori precedenti, la stessa cosa che noi italiani chiamiamo prodotto vettoriale e che restituisce la normale, cioè la perpendicolare, tra i due vettori precedenti. Siccome abbiamo fatto puntare i vettori verso il punto 4, ci tocca invertire il segno della normale, da cui:
var x_ab_bc :Vector3 = -ab.cross(bc)Qualcuno potrebbe far notare che bastava invertire le differenze usate per calcolare i vettori ab e bc per poter ottenere la normale direttamente con il segno giusto e sarebbe pure vero, però io ho imparato da Sebastian Langue: casomai quello un po’ sciroccato è lui… No, scherzo dai! E’ solo la scusa per dargli giusti onori e glorie! Sebastian è un punto di riferimento davvero formidabile per tutorials di alto livello che trattano questa materia. Vi lascio il link al suo canale su YouTube2 in calce, come al solito. Fatevi un giro e iscrivetevi. Sebastian è un vero hacker nel mondo dei videogiochi, cosa che dimostra puntualmente con i suoi code adventures.
Torniamo a noi. Abbiamo ragionato su una singola coppia di direzioni, ma il processo va ripetuto per ogni punto. Quindi, prendiamo le direzioni che dall’esterno convergono verso un punto, ne facciamo il prodotto vettoriale e lo mettiamo da parte. Otterremo tre normali diverse, giusto? Cosa ne facciamo? La media, verrebbe da dire. Ma qui non ce n’è traccia:
var sum_normal: Vector3 = x_ab_bc + x_bc_ca + x_ca_abQui c’è solo una somma. La media dovete tenerla in testa, perché è quello che andrebbe fatto. Il vero motivo per cui non lo facciamo è che, leggendo bene il codice, noterete che ogni punto potrebbe essere interessato da somme successive. Il punto numero 5, verrà modificato sia quando i varrà 0 che quando i varrà 1. Quindi, per ogni punto, stiamo accumulando lo spostamento della normale uscente. Immaginatevi queste frecce che spuntano fuori dai singoli punti. A mano a mano che procedete nei calcoli crescono di valore, ma non ve ne frega niente. Invece è interessante vedere come cambia la loro pendenza verso i singoli assi a mano a mano che si sommano ulteriori informazioni, chiaro?
Alla fine, la somma ottenuta è aggiunta ai valori precedenti e non sostituita! Partite dal presupposto che, quando è inizializzato per la prima volta, l’array delle normali contiene tutti valori pari a zero. Vedete qui:
normals[indices[a]] += sum_normal
normals[indices[a + 1]] += sum_normal
normals[indices[a + 2]] += sum_normalAd ognuna delle normali è sommato il risultato di questo ciclo, che è lo stesso per tutti e tre i punti dello stesso triangolo. Il singolo punto, però, verrà influenzato da i calcoli che interessano tutti i triangoli che lo contengono! E le pendenze diventeranno la media di tutte, di conseguenza.
Dicevo che delle dimensioni non ci frega nulla giusto? Ce ne frega talmente poco, che l’ultimo ciclo, si ripassa tutte le normali e le normalizza. Ecco il motivo per cui non siamo interessati ai valori, ma solo alle pendenza: le normali ci piacciono… normalizzate.
Finalmente il nostro benchmark
Il codice contiene altre informazioni, non tantissime per la verità. E’ chiaro che questo tutorial è per molti, ma non per tutti: richiede una certa esperienza. Troverete da soli che, come al solito, abbiamo creato qualcosa che poi siamo andati a distruggere: una MeshInstance3D al cui parametro mesh è assegnato proprio l’ArrayMesh che siamo andati a costruire con tutto il resto del codice, quello che abbiamo commentato fino a qui.
Non mi ripeto neanche per ciò che concerne le registrazioni delle classi sul lato C++. La classe C++ non l’ho neanche visualizzata, questa volta, perché è troppo lunga per starci in una sola immagine. Ad ogni modo, se vi siete scaricati da mio account GitHub (link nella barra del titolo in alto) il codice, dovreste poterla vedere da soli. La classe si chiama GDBenchmarkPromisedLand seguendo le convenzioni che ci siamo dati fin qui ed è suddivisa tra due files con le canoniche estensioni del mondo C++.
Vale anche la considerazione a livello grafico: se volete vedere il terreno, per convenienza, disattivate l’ultima parte del codice, GDScript, quella che distrugge la classe MeshInstance3D che lo contiene, e disattivate pure il benchmark di GDBenchmarkPromisedLand per evitare che i due risultati si accavallino tra loro. Potete anche fare il contrario, tenendo conto, però, che ogni modifica al codice in C++ deve essere seguita da ricompilazione via SCons.
Bene, allora! Lo lanciamo questo benchmark? Otteniamo:
— GDScript ha generato un piano di 250000 punti
Terra promessa in GDScript –> 554075 usec.
— GDExtension ha generato un piano di 250000 punti
Terra promessa in GDExtension –> 72016 usec.
Sento suonare le campane nel cielo, alleluia!
- Link ufficiale alla voce dedicata ad ArrayMesh nella guida di Godot (spero) ↩︎
- Link al canale YouTube di Sebastian Langue, un vero hacker del mondo dei videogiochi ↩︎


